N = (2xy x 2 − 2) For a differential equation to be an exact differential equation, we need condition M y = N x M y = 2 (x y) N x = 2y 2x = 2 (x y) So, the given equation is an exact differential equation We are looking for the solution of the form Ψ (x, y) = C dΨ = Ψ x dx Ψ y dy = 0 ⇒Ψ x = (x y) 2 and Ψ y = (2xy x 2Equation is exact, so we can find F(x,y) such that Fx = M, Fy = N F(x,y) = ∫ M(x,y) dx F(x,y) = ∫ (x y)² dx F(x,y) = ∫ (x² 2xy y²) dx F(x,y) = 1/3 x³ x²y xy² g(y) F(x,y) = ∫ N(x,y) dy F(x,y) = ∫ (2xy x² − 3) dy F(x,y) = xy² x²y − 3y h(x) Comparing both values we see that h(x) =Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
Solve The Differential Equation X 2 1 Dy Dx 2xy 1 X 2 1 Sarthaks Econnect Largest Online Education Community
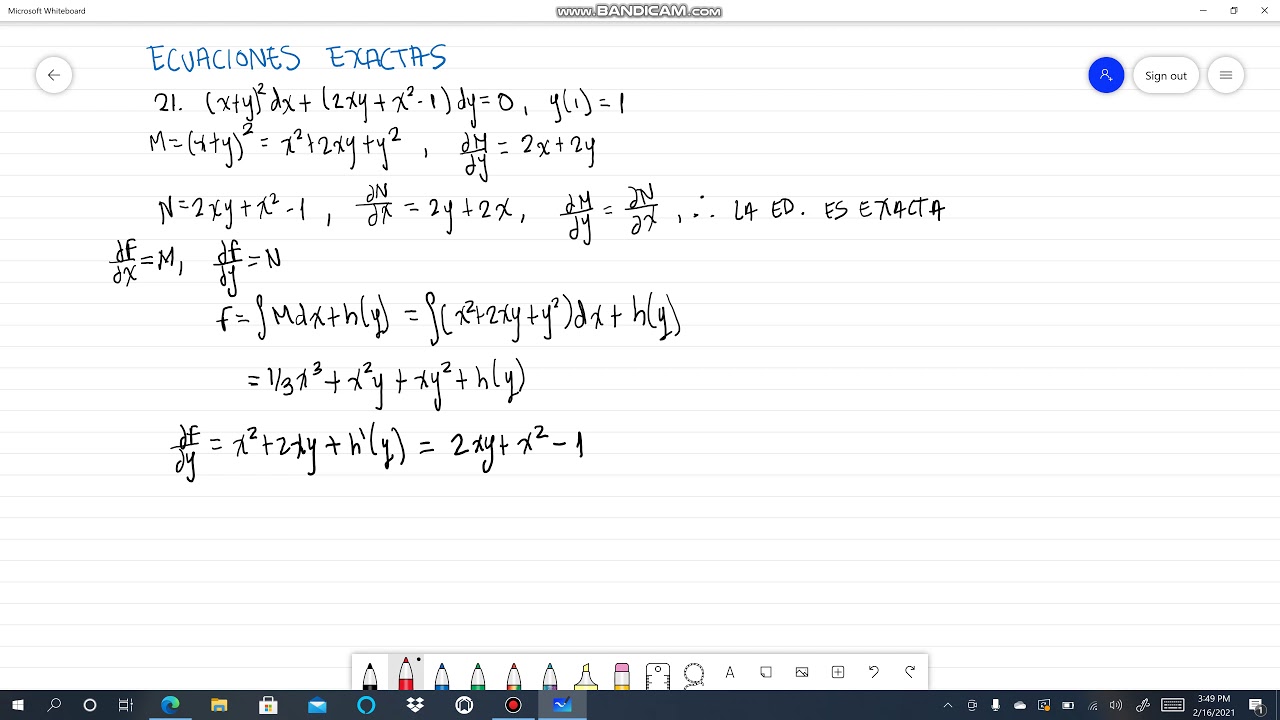
X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1
X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1- In differential equation show that it is homogeneous and solve it dy/dx = 2xy/(x^2 y^2) asked in Differential Equations by Devakumari (Regard y as independent variable and x as dependant variable and find the slope of the tangent line to the curve (4x^2 2y2)^2 x^2y = 45 at point (3,4) Correct answer is Here's what I did 2(8x(dy/dx)
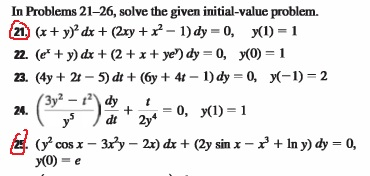



Solved In Problems 21 26 Solve The Given Initial Value Chegg Com
Consider the following initialvalue problem (x y)2 dx (2xy x2 − 8) dy = 0, y(1) = 1 Let ∂f ∂x = (x y)2 = x2 2xy y2 Integrate each term of this partial derivative with respect to x, letting h(y) be an unknown function in y f(x, y) = 13 x3x2yxy2 h(y) Find the;Scribd es red social de lectura y publicación más importante del mundo Scribd es red social de lectura y publicación más importante del mundo Abrir el menú de navegación Cerrar sugerencias Buscar Buscar es Change Language Cambiar idiomaThis problem has been solved!
Solution for 2 (2xy x)dy – x² y² y 1dx = 0 Whenx = 1;Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepFind the particular solution of the differential equation (1 – y^2) (1 log x) dx 2xy dy = 0, given that y = 0 when x = 1 CBSE CBSE (Commerce) Class 12 Question Papers 1799 Textbook Solutions MCQ Online Tests 29 Important Solutions 3664 Question Bank Solutions
If 3x^22xyy2=2 then the value of dy/dx x = 1 is A 2 B 0 C 2 D 4 E not defined algebra The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle; Explanation dy dx = 1 2xy ∴ dy dx −2xy = 1 1 This is a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;=0 when =1 (1 x2) 2xy = 1 1 2 divide both sides by (1 2) 2 1 2 = 1 1 2 (1 2) 2 1 2 y = 1 1 2 comparing with py = q p = 2 1 2 & q = 1 1 2 2 find integrating



Solve The Following Differential Equation 1 X 2 Dy Dx 2xy 1 1 X 2 Given Y 0 When X 1 Sarthaks Econnect Largest Online Education Community




Engineering Mathematics Notes
1年前 求椭球面x^22y^2x^2上平行于平面xy2z=0的切平面方程 1年前 口腔属于消化道吗? 1年前 设两个相互独立的随机变量X和Y分别服从正态分布N(0,1)和N(1,1),则( ) 1年前The ode is exact so it has a solution of the form Choose so that David Kaplan Mathematics Professor (1990–present) Author has 455 answers and 1576K answer views 8 mo Related What is the general solution of x^2 dx y (x1) dy=0? (x 2 y 2 ) dx 2xy dy = 0 given that y = 1 when x = 1 differential equations;



Differential Equations




Solved I Linear Equation Of Order One 1 Xdy Y Xy 2 Dx Chegg Com
Solution for (A) (xy)* dx(2xy x² –1)dy = 0, y(1) =1 close Start your trial now!(y^22xy)dx=(x^22xy)dy Get the answers you need, now!The given Equation is an exact differential equation Solution is given by ∫ M d x ∫ ( T e r m s i n N n o t c o n t a i n i n g x) d y = c y=constant ∫ ( 1 y − 2 x) d x ∫ 3 y d y = c x y − 2 log x 3 log y = c ADD COMMENT EDIT Please log in to add an answer



Proverte Moyo Reshenie Dnevniki Asocialnaya Set




Solved For Problems 26 Determine An Integrating Factor Chegg Com
解:∵(3x^2y2xyy^3)dx(x^2y^2)dy=0 ==>(3x^2ydx2xydxx^2dy)(y^3dxy^2dy)=0 ==>(3x^2ye^(3x)dx2xye^(3x)dxx^2e^(3x)dy)(y^3e^(3x)dxy^2e^(3x)dy)=0 (等式两端同乘e^(3x)) ==>d(x^2ye^(3x))d(y^3e^(3x))/3=0 ==>x^2ye^(3x)y^3e^(3x)/3=C/3 (C是积分常数)The differential equation 2xydy=x 2y 21dx determines A A family of circles with centre on xaxis B A family of circles with centre on yaxis C A family of rectangular hyperbiola with centre on xaxis D A family of rectangulat hyperbola with centre on yIntegrating Factors Some equations that are not exact may be multiplied by some factor, a function u (x, y), to make them exact When this function u (x, y) exists it is called an integrating factor It will make valid the following expression ∂ (u·N (x, y)) ∂x
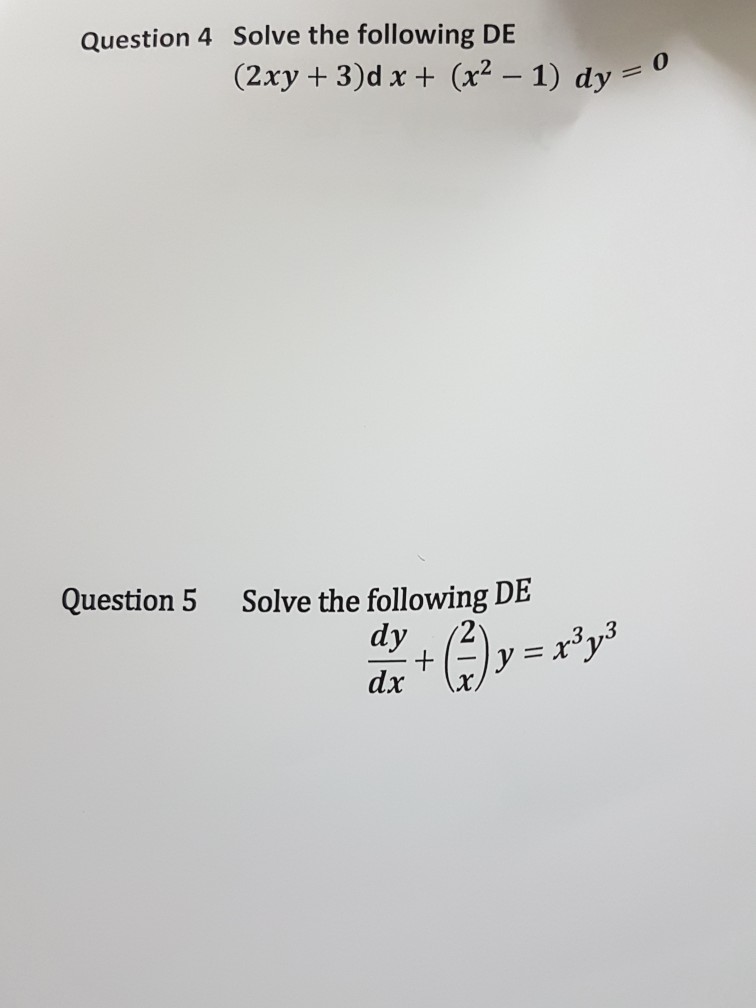



Solved Solve The Following De 2xy 3 D X X 2 1 Dy Chegg Com




Math 432 Hw 2 5 Solutions Frostburg
Arrow_forward learn write tutor study resourcesexpand_more Study Resources We've got the study and writing resources you need for your assignments Start exploring!Q Q4 (a) Solve the Differential equation (x 1) – y(2xy 3y^2)dx (2xy x^2)dy = 0 Natural Language;



Solve The Following Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1 Sarthaks Econnect Largest Online Education Community




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5
Solution Verified by Toppr Correct option is B) dxdy= 2xyy 2−x 2 Substitute y=vx ∴vx dxdv= 2vv 2−1⇒x dxdv=− 2v1v 2⇒ 1v 22v dv xdx=0 Integrating log(1v 2)logx=logk ∴x(1v 2)=k Substitute v= xy ⇒x 2y 2=kx Video Explanation Solve any question of Differential Equations with Patterns of problems > Was this answer helpful?Share It On Facebook Twitter Email 1 Answer 2 votes answered by rubby (525k points) selected by Vikash Kumar Best answer Integrating both sides, we get ex 96, 14 for each of the differential equations given in exercises 13 to 15 , find a particular solution satisfy the given condition 1 2 2 = 1 1 2 ;




If Sin Y Dy Dx Cos X 2cos Y Sin 2x And Y 0 Pi 2 Then 198 E 2 4cos Y Pi 2 Is Equal To




Y 1 Y 2 Y 3 Hotsell 51 Off Empow Her Com
2xydx (y23x2)dy=0 Geometric figure Two Straight Lines Slope = 1 xintercept = 0/1 = yintercept = 0/1 = Slope = 00/00 = This is my attempt \\frac{dy}{dx} = \\frac{y^2 1}{x^2 1} \\\\ \\int \\frac{dy}{y^2 1} = \\int \\frac{dx}{x^2 1} \\\\ \\ln \\left \\frac{y1}{y1} \\rightThe functions f, g and h satisfy the relations f (x) = g(x 1) Then f " (2x) is equal to Answer 9 If x = sin − 1(3t − 4t3) and y = cos − 1(√1 − t2), then dy dx is equal to Answer 10 If y2 = 100tan − 1x 45sec − 1x, then dy dx = Answer 11 If y = sin − 1√1 − x, then dy dx is equal to Answer 12



How To Solve The Initial Value Problem Ivps Dy Dx Y 2x X Y Y 1 2 Quora




Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity
Join this channel to get access to perkshttps//wwwyoutubecom/channel/UCFhqELShDKKPv0JRCDQgFoQ/joinHere is the technique to solve this question and how toFirst week only $499!See the answer Solve the given initialvalue problem ( x y) 2dx (2 xy x2 − 6) dy = 0, y (1) = 1 Expert Answer 92% (26 ratings) Previous question Next question




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True A Solution Is X 2 Y 2 Cx B X 2 Y 2 Cx C X 2 Y 2 X C D Y 0 0



Solved A Solve 2xy Cos X 2 2xy 1 Dx Sin X 2 X 2 Dy 0 B Course Hero
See answers (1) asked x ˙ = r x − h x 2 q, where x ˙ = d x d t I'm assuming r, h, q have different units I first tried τ = t t 0 and A = x x 0 Then I got d A x 0 d τ t 0 = r A x 0 − h A 2 x 0 2 qWhat is the solution of (xy^2) dx 2xy dy = 0?Separate the variables ydy = x^2 / (x 1)dx Divide x^2 by x 1 to get



X Y 2 Y 2 Dx X 2 X 2 Y Dy 0 How Do You Solve The Differential Equation Quora



How To Solve Math X Y 2 Dx 2xy Dy 0 Quora
JEE Main 19 The solution of the differential equation , (dy/dx) = (xy)2 , when y(1) = 1, is (A) loge (2y/2x) = 2 (y1) (B) loge (2x/2y) =Ravinenavath869 ravinenavath869 Math Secondary School (y^22xy)dx=(x^22xy)dy 1 See answer ravinenavath869 is waiting for your help Add your answer and earn pointsCalculus Find dy/dx x^2y^2=2xy x2 y2 = 2xy x 2 y 2 = 2 x y Differentiate both sides of the equation d dx (x2 y2) = d dx (2xy) d d x ( x 2 y 2) = d d x ( 2 x y) Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps
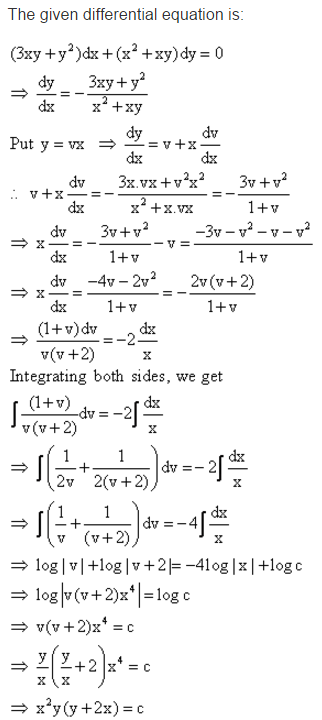



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Maths Topperlearning Com D1ksg633



How To Solve The Differential Equation 2x Y Dx 4x Y 6 Dy 0 Quora
Dy dx P (x)y = Q(x) This is a standard form of a Differential Equation that can be solved by using an Integrating Factor I (X^22xyy^2)dx(xy^2)dy=0 1 See answer ssirissiri97 is waiting for your help Add your answer and earn pointsThis helps us sort answers on the page Absolutely not Definitely yes



Solved A Solve 2xy Cos X 2 2xy 1 Dx Sin X 2 X 2 Dy 0 B Course Hero



Solved Find The Particular Solution Of Y 2x 2 Xy Y 2 Dx X 2 2x 1 Dy 0 Course Hero
How do you solve linear firstorder differential equations? Transcript Ex 95, 4 show that the given differential equation is homogeneous and solve each of them ( ^2 ^2 ) 2 =0 Step 1 Find / ( ^2 ^2 ) 2 =0 2xy dy = ( ^2 ^2 ) dx 2xy dy = ( ^2 ^2 ) dx / = ( ^2 ^2)/2 Step 2 Putting F(x, y) = / and finding Solution Given equation is (2xyytany)dx (x 2 xtan 2 ysec 2 y)dy=0 Step 1 Comparing with Mdx Ndy = 0 M= 2xyytany and N = x 2 xtan 2 y Step 2 Check ∂M/∂y = ∂N/∂x ∂M/∂y = 2x1sec 2 y = 2xtan 2 y ∂N/∂x = 2xtan 2 y Therefore ∂M/∂y = ∂N/∂x Step 3 The general solution of equation 1 is



Solved Solve The Following Differential Equations 1 X Y 3 Dx Course Hero



Solved Find The General Solution Of The Differential Equation 3 Y X 2 2 X Y Y 3 D X X 2 Y 2 D Y 0 Course Hero
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyX and y are positive integers; y = (xlnx)/(1lnx) We have dy/dx = (x^2y^2xy)/x^2 with y(1)=0 Which is a First Order Nonlinear Ordinary Differential Equation Let us attempt a substitution of the form y = vx Differentiating wrt x and applying the product rule, we get dy/dx = v x(dv)/dx Substituting into the initial ODE we get v x(dv)/dx = (x^2(vx)^2x(vx))/x^2




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy




Engineering Mathematics Notes
2 Answers { x 2 − y 2 = r 2 cos ( 2 θ) 2 x y = r 2 sin ( 2 θ) d x = cos ( θ) d r − r sin ( θ) d θ d y = sin ( θ) d r r cos ( θ) d θ When you report in the ODE, you can cancel the factor r 2, also collecting d r and d θ you'll find addition formulas for angle ( 2 θ − θ) and you will eventually getFind the particular solution of the differential equation dy/dx=(xy)/(x^2y^2) given that y = 1, when x = 0 CBSE CBSE (Commerce) Class 12 Question Papers 1799 Textbook Solutions MCQ Online `⇒−x^2/(2y^2)lny=C` Given y = 1 when x = 0 ⇒ C = 0 Thus, the particular solution of the given differential equation is given by `lnyGet an answer for 'solve the differential equation (2xy3y^2)dx(2xyx^2)dy=0 ' and find homework help for other Math questions at eNotes
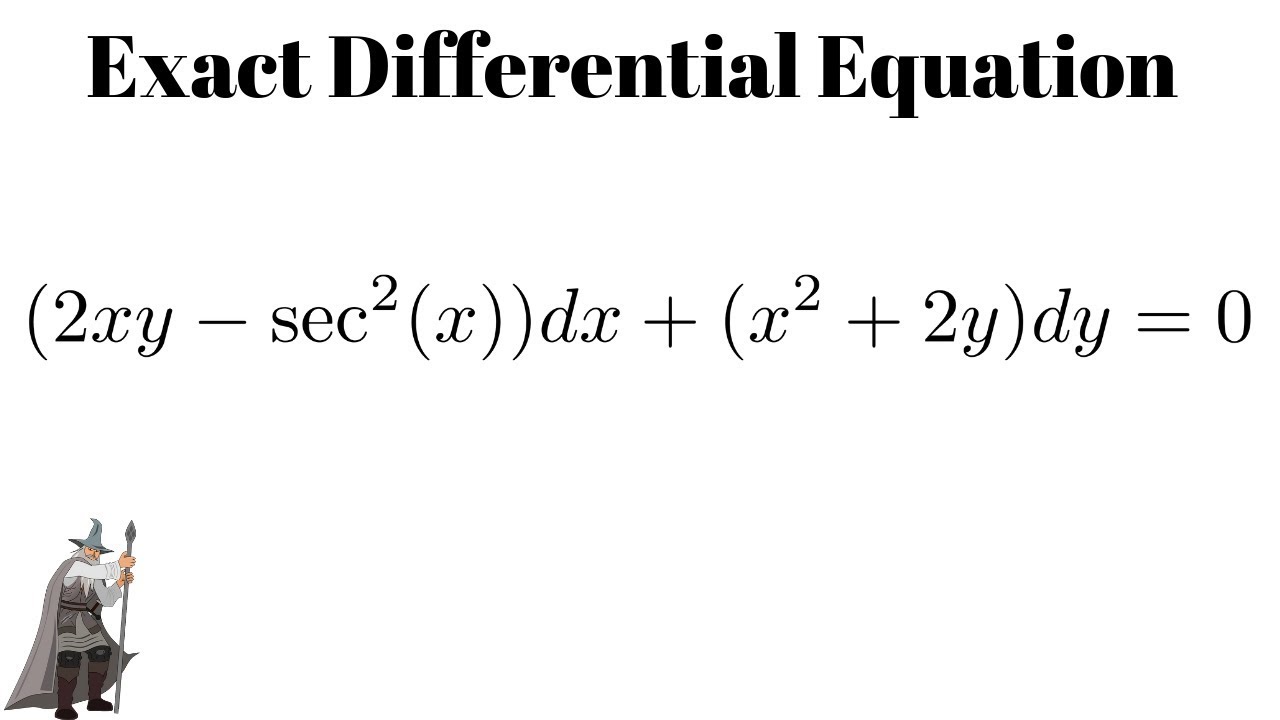



Exact Differential Equation 2xy Sec 2 X Dx X 2 2y Dy 0 Youtube



1
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepWe have differential equation of the form M (x,y) dx N (x,y) dy = 0 Equation is exact if ∂M/∂y = ∂N/∂x M (x,y) = xyy²y —> ∂M/∂y = x2y1 N (x,y) = x²3xy2x —→ ∂N/∂x = 2x3y2 Equation is not If y = x (mod N 1 ) and gcd(x,n) = 1, then why is itY = 0 %3D Bernoulli's or Linear Equation Solve for the particular solution of the given differential equation




Solve Y 2xy 1 Dx X 1 2xy X 2y 2 Dy 0
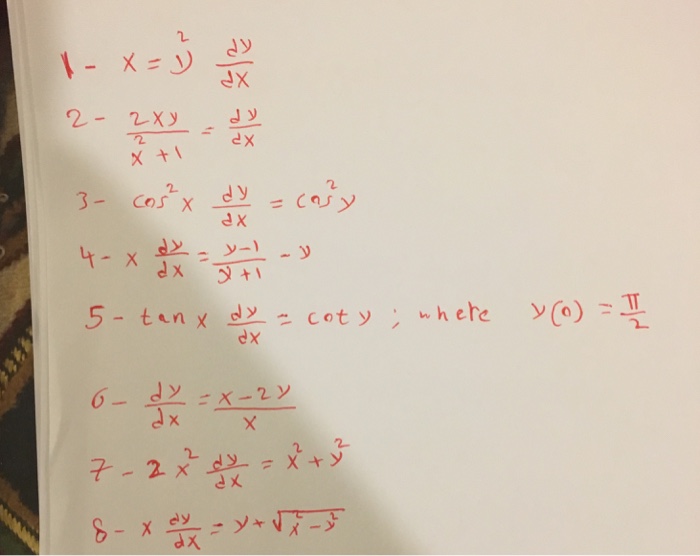



Solved X Y 2 Dy Dx 2xy X 2 1 Dy Dx Cos 2x Dy Dx Chegg Com
The equation y (y^21)dx x (y^2 1)dy =0 ,is directly separated as (y^2–1)dy/y (y^21) = dx/x Obtain dx/x = 2ydy/ (y^21) dy/y Integrating gives lnx = ln (y^21) iny lnC Then the solution is x (y^21)/y = K Your response is private Is this a valuable answer?Explanation Given Expression 3x 2 2xy y 2 = 2 When x = 1 then y = 1 by substituting the value of x in the above expression Differentiating on both the sides of the given expression with respect to x, we get (d / dx) (3x 2 2xy y 2) = (d / dx) (2)Calculus Examples Popular Problems Calculus Find dy/dx x^2xyy^2=1 x2 − xy y2 = 1 x 2 x y y 2 = 1 Differentiate both sides of the equation d dx (x2 −xy y2) = d dx (1) d d x ( x 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps



How To Solve Math X Y 2 Dx 2xy Dy 0 Quora




1 1 X 2 Dy 2x Y 3 Dx 0 Y 1 X 0 2 4
Ecuacion diferencial de primer orden` (x^(2)y^(2)) dx 2xy dy = 0`




Solve The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1



Solve The Differential Equation X 2 1 Dy Dx 2xy 1 X 2 1 Sarthaks Econnect Largest Online Education Community



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Maths Topperlearning Com 237hoo




Ex 9 6 8 Find General Solution 1 X2 Dy 2xy Dx Ex 9 6



How To Solve X Y Dx 2xydy 0 Quora



Solve The Differential Equations 1 X 2 Dy Dx 2xy X 1 X 2 Sarthaks Econnect Largest Online Education Community



How To Solve The Differential Equation X Y Dx Y 2xy X Dy 0 Quora




Solution Of The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Is Youtube




First Order Differential Equations Ppt Download



What Is The Homogeneous Equation Of 2xy Y 2 Dx X 2 Xy Dy Quora




Solved In Exercises 0 Determine Whether Or Note Each Of The Given Equations Is Exact Solve Those That Are Exact 3x 2y Dx 2x Y Dy 0 Y
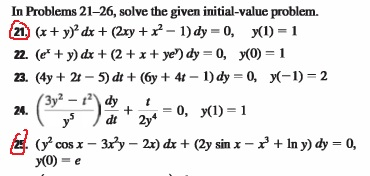



Solved In Problems 21 26 Solve The Given Initial Value Chegg Com




Engineering Mathematics Notes



Solve Xy 2x Y 2 Dx X 2 2x Dy 0 Separable Equation Differential Equation Youtube




Math 432 Hw 2 5 Solutions



1




Solve Dy Dx 2x Y 1 X 2y 3 Youtube
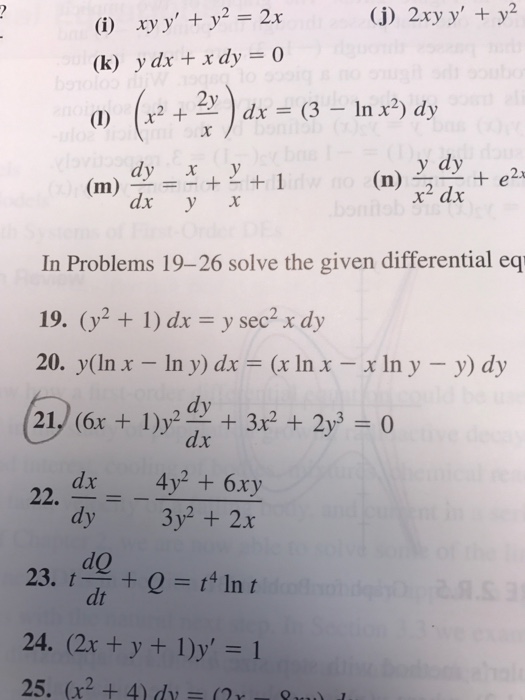



Solved Xy Y Y 2 2x 2xy Y Y 2 Y Dx X Dy 0 X 2 Chegg Com
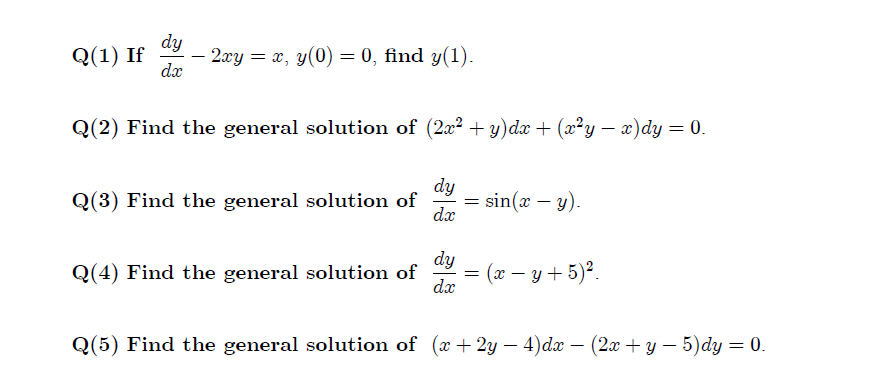



Solved Q 1 If Dy Dx 2xy X Y 0 0 Find Y 1 Q 2 Find Chegg Com




Solved In Solve The Given Initial Value Problem X Y 2 Chegg Com




2xy Dy Dx X 2 3y 2 Youtube



The Solution Of 1 X 2 Dy Dx 2xy 4x 2 0 Is Sarthaks Econnect Largest Online Education Community



Solved Solving Exact First Oder Differential Equations Course Hero




Math 432 Hw 2 5 Solutions




In The Following Show That The Given Differential Equation Is Homogeneous And Solve Each Of Them 1 X 2 Xy Dy X 2 Y 2 Dx 2 Y X Yx




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Solved Y Ln Y X 2 1 Dy Dx 2xy Y 1 X 2 Y 2 4 Chegg Com



Solved Please See An Attachment For Details Course Hero




Math 432 Hw 2 4 Solutions Frostburg




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



What Is The Solution Of 2 2xy 4y 3 Dx X 2 2 Dy 0 With An Answer Of Y 2 X 2 1 C X 2 4 Quora
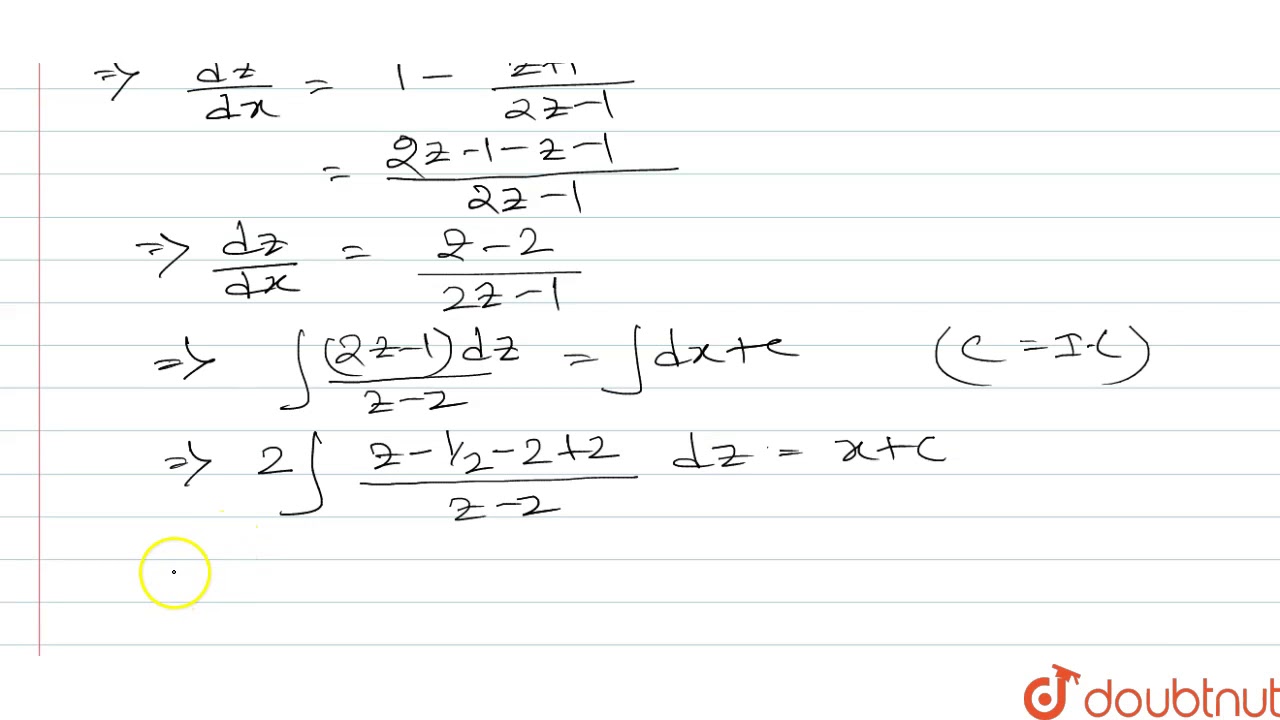



X Y 1 Dx 2x 2y 1 Dy 0 Youtube




The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 1 Sqrt 1 X 2 C B Y 1 X 2 Sqrt 1 X 2 C C Y 1 X 2 3 2 Sqrt 1 X 2 C D None Of These




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube



21 X Y 2 Dx 2xy X 2 1 Dy 0 Y 1 1 Ecuaciones Exactas Alexander Estrada Youtube



Solved Solve The Following Ordinary Differential Equation Course Hero




Solved Consider The Initial Value Problem Dy Dx 2xy X Chegg Com



Solve X 2 Y 2 Dx 2xy Dy 0 Sarthaks Econnect Largest Online Education Community



What Is 2x Y 1 Dx 2y X 1 Dy Quora




Solved In Problems 21 26 Solve The Given Initial Value Chegg Com




Solve Y 1 2xy Dx X 1 Xy Dy 0




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Solved I 2x Y 1 Dx Ydy 0 Ii Xydx X2 Y2 Dy 0 Chegg Com




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy
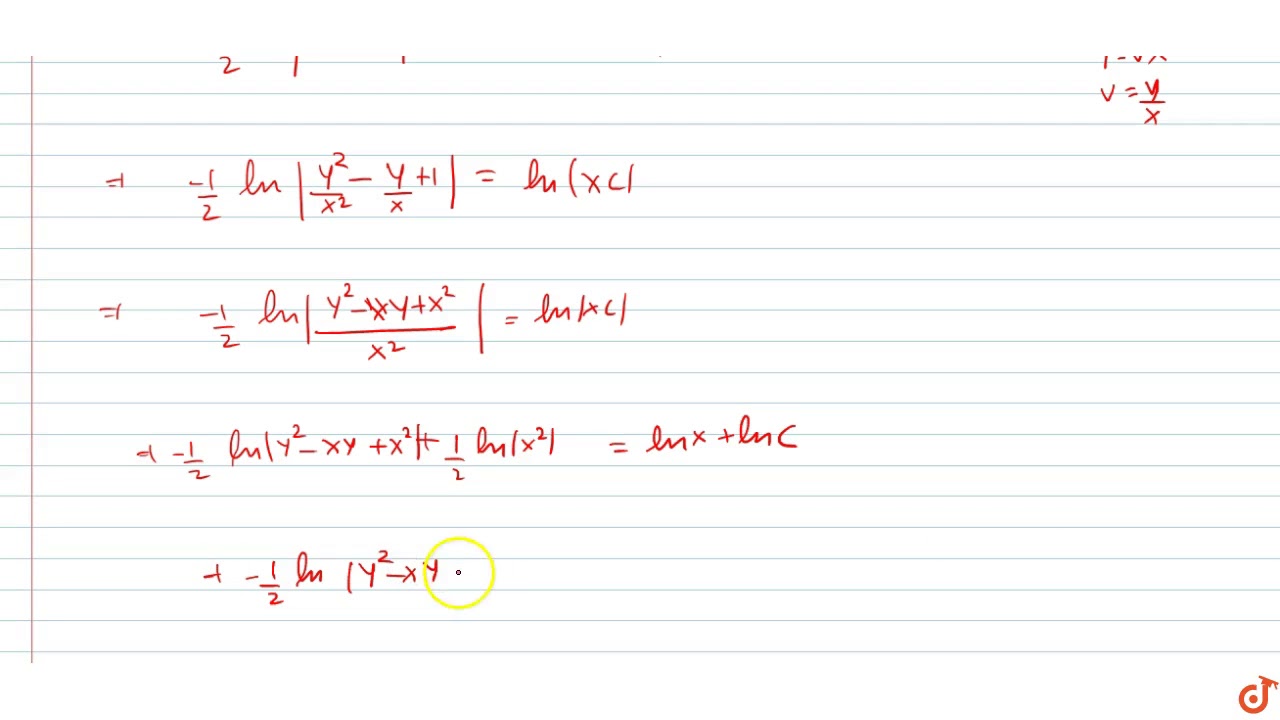



2x Y 1 Dx 2y X 1 Dy 0 Youtube




Solving Differential Equation 2xy Dy Dx Y 2 X 2 0 Youtube




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy
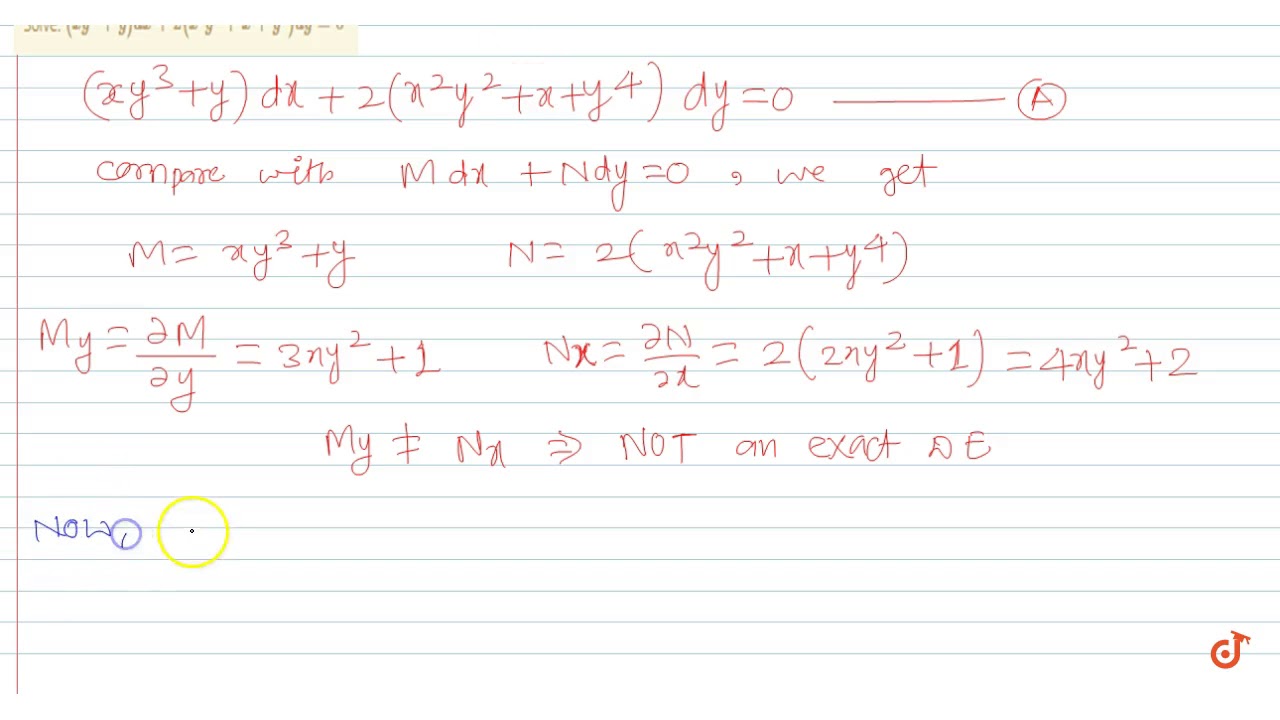



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube



Solved Test Exactness And Solve Question 1 2xy 3x 2 Dx X 2 2y Dy 0 Question 2 Cosx Xsinx Y 2 Dx 2xydy 0 Question 3 2xydx X 2 Course Hero




Solve The Following Differential Equations 1 X2 Y2 Dx 2xy Dy 3 Xly Dx 2 Y2 Dy 0 V T U 10 6 Y2 X2 Dx Xy Day Wegglab




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis



What Is The General Solution Of The Differential Equation 2xy Y 2 Siny Dx X 2 Xy 2 Cosy Dy 0 Quora




1 X 2 Dy Dx 2xy X 2 2 X 2 1 Youtube




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



How To Find The Exact Solution To X Y 2 Dx 2xy X 2 1 Dy 0 Using Partial Derivatives Quora



How To Complete 2xy Sinx Dx X 2 Cosy Dy 0 Quora



How To Solve X Y Dx 2xydy 0 Quora



Solve 1 X 2 Dy Dx 2xy 4x 2 0 Subject To The Initial Condition Y 0 0 Sarthaks Econnect Largest Online Education Community
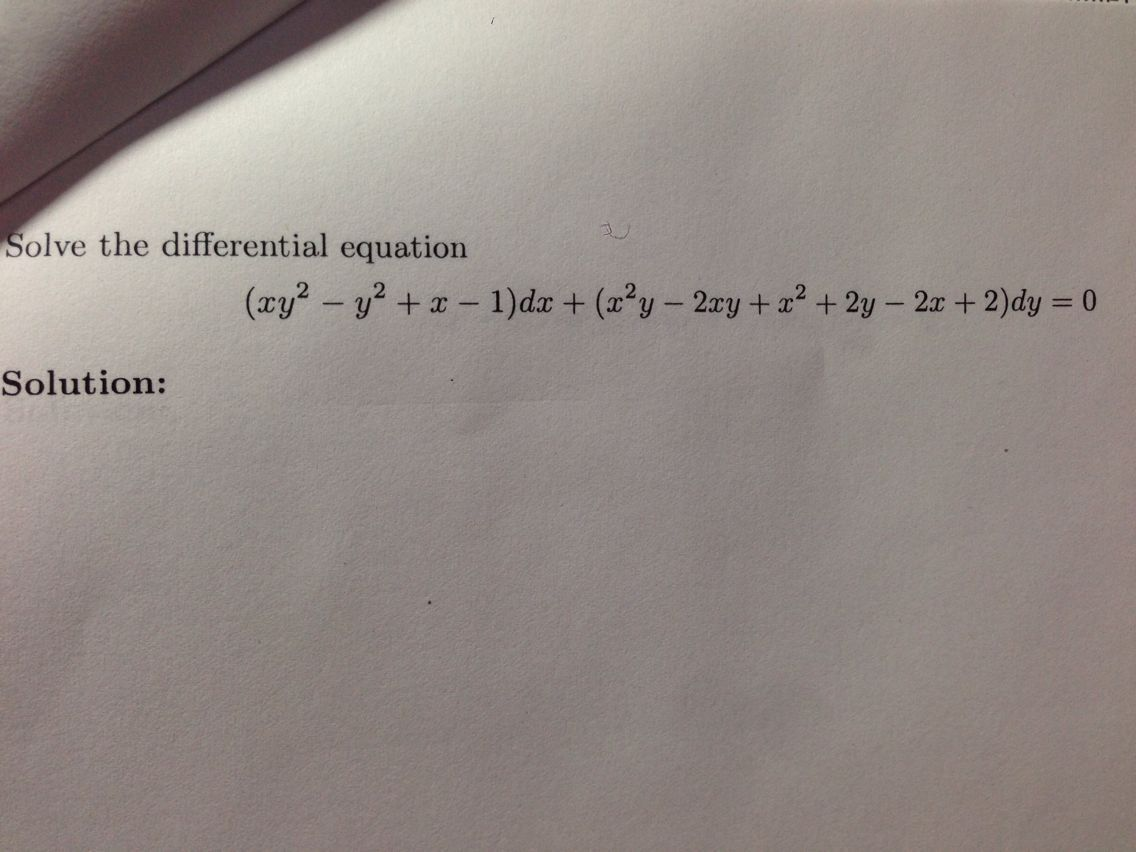



Solved Solve The Differential Equation Xy 2 Y 2 X Chegg Com




Engineering Mathematics Notes
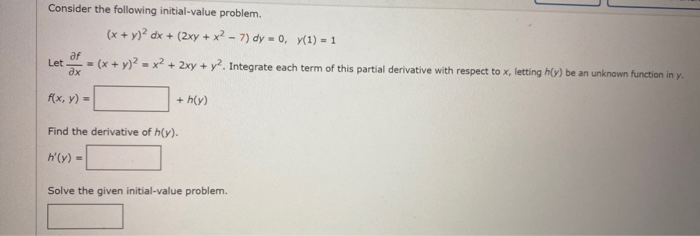



Solved Consider The Following Initial Value Problem Af Let Chegg Com



How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora




Solve Y 1 Xy Dx Xdy 0 Youtube


