Graph the parabola {eq}y = 2x^2 12x 16 {/eq} Parabola A parabola is a Ushaped graph, which may open in any direction The direction of opening is described by the value of "a" in theThe directrix of a parabola is the vertical line found by subtracting from the xcoordinate of the vertex if the parabola opens left or right Substitute the known values of and into the formula and simplify Use the properties of the parabola to analyze and graph the parabolaParabola, Finding the Vertex 51 Find the Vertex of y = 2x 2 5x2 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 2 , is positive (greater than zero)

Solution Find The Equation Of The Axis Of Symmetry Of The Function Y 2x 2
Y=(x-2)^2-3 parabola
Y=(x-2)^2-3 parabola-A ≠ 0 then the xcoordinate of the vertex is ∙ xxvertex = − b 2a y = 2x2 10x 8 is in standard form with a = 2,b = 10 and c = 8 ⇒ xvertex = − 10 4 = − 5 2 substitute this value into the equation for ycoordinate yvertex = 2( − 5 2)2 10( − 5 2) 8 Refer explanation section Given y=2x^24 To find the vertex, rewrite the function as y=2x^x4 xcoordinate of the vertex x=(b)/(2a)=0/(2 xx 2)=0 y coordinate of the vertex At x=0;



Exploration Of Parabolas
The parabola `y=x^(2)pxq` intersects the straight line `y=2x3` at a point with abscissa 1 If the distance between the vertex of the parabola nad the XaxParabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose theThe "formula" for a parabola (in the conic sections form) is mathx^2=4cy/math (although some textbooks use mathp/math instead of mathc/math, so mathx^2=4py/math) If you put your equation into that form you can make some observatio
The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetryThe focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focusThis is an equation of the standard form for a parabola y=A (xh)^2k, with (h,k) being the (x,y) coordinates of the vertex For given equation vertex (0,6) negative lead coefficient means parabola opens downwards yintercept set x=0 y=6
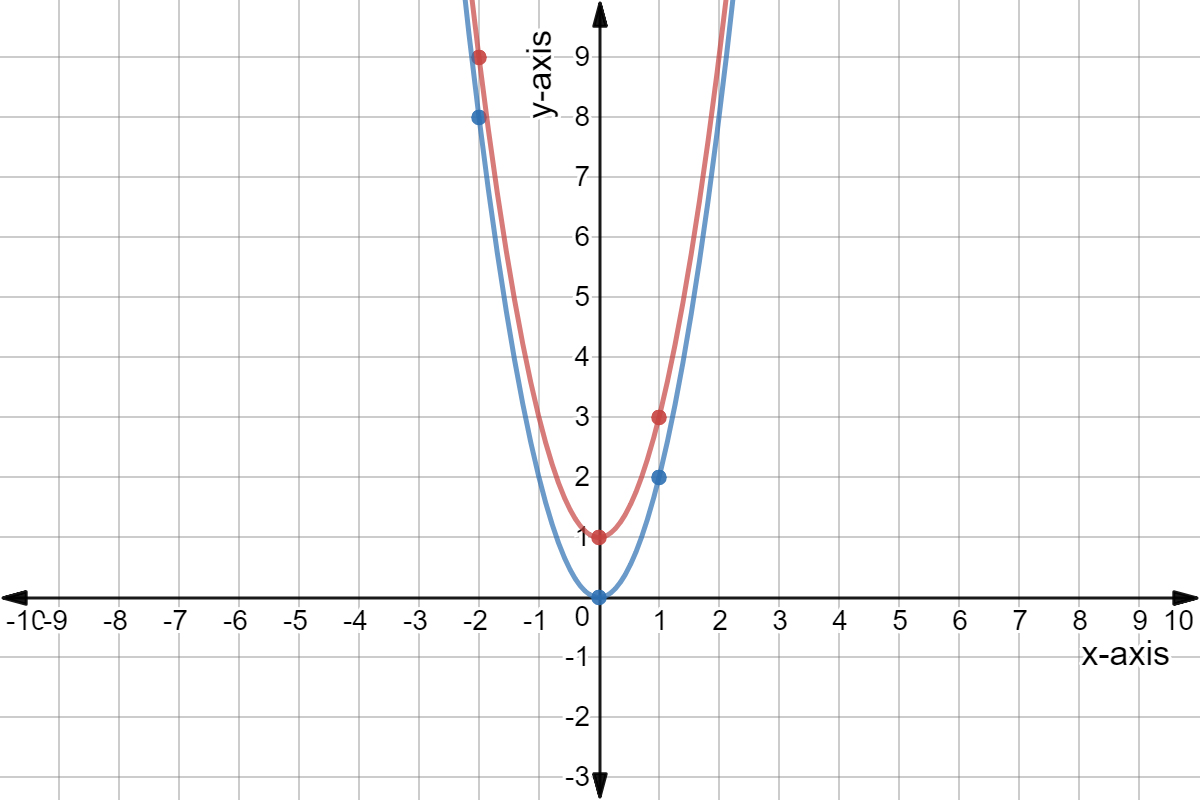
Exploration of Parabolas By Thuy Nguyen In this exploration we want to see what happens when we construct the graphs for the parabola y = ax 2 bx c with different values of a, b, and c We'll start first by constructing the graphs for y = ax 2 with different values of a The following are graphs for a = 2, 1, 2, in blue, purple, and red respectivelyY=2(0)^(0)4=4 Vertex (0, 4) y Intercept (0, 4) To find the xintercept put y=0 2x^24=0 2x^2=4 x^2=(4)/2 x=sqrt(4)/2 The function has imaginary roots It means, it doesn't have xParabola PreÁlgebra Orden (jerarquía) de operaciones Factores y números primos Fracciones Aritmética Decimales Exponentes y radicales Módulo Media, parabolaequationcalculator y=2x^{2} es Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




The Slope Of The Tangent Line To The Parabola Y 2x Gauthmath
{eq}y= 2x^2 4x 8 = 0 {/eq} Parabolas The equation of a parabola is a quadratic equation whose points are all the same distance from a focus point and a directrix lineShort demo on graphing a parabola by finding the vertex and yintercept, and using the axis of symmetryExploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts




Please Help Thank You The Graph Of The Function Y X2 Is Shown How Will The Graph Change If Brainly Com



Sketching Quadratics
Also graph the parabola If you can please include the points that I have to graph/plot that would be great I know how to get the vertex but I always mess up when it comes to graphing the exact point or points Answer by ewatrrr() (Show Source)Answer and Explanation 1 Become a Studycom member to unlock this answer!Click here👆to get an answer to your question ️ The focus of the parabola y = 2x^2 x is Join / Login maths The focus of the parabola y = 2 x 2 x is A If A (2, 0) is the vertex and the yaxis is the directrix of a parabola, then its focus is View solution



Solved Which Shape Is Defined By The Equation Y 2x 2 3 Course Hero



How To Represent The Graph Of The Parabola Y 2 4x Quora
Y=2x^26 How do I graph this? Forget 0 that's a local maximum So, the distance from the parabola to C is ‖(1 2, 1) − (3 2, 0)‖ = √2 Any point of the parabola is of the type (x, Y) with y2 = 2x The distance between (x, y) and (15, 0) is √(x − 15)2 y2 = (x − 15)2 2x You have to find the minimum value of this quantity over all x ≥ 0 x = (y2 / 2Parabola, Finding the Vertex 31 Find the Vertex of y = 2x 212x15 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 2 , is positive (greater than zero)



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic



What S The Axis Of Symetry Vertex And Graph Y 2x 2 6x 1 Mathskey Com
The parabola is f(x) = y = 2x 2 4x 3 Write the equation in vertex form of a parabola eqaution Divide each side by negative 2 y/2 = x 2 2x 3 /2 To change the expression x 2 2x 3 /2 into a perfect square trinomial add and subtract (half the x coefficient) The parabola has the equation y=2x^2x If y=ax^2bx then y'=2axb This gives us our slope of y at any given x So at the point (1,1), the slope must be y'=2a(1)b=2ab We know the slope must also be 3 at the point (1,1), to match the linear equation given Thus, these two slope values must be equal 2ab=3 1 We also know that (1,1) is a point on the parabola, so it mustStep 1 Finding the Vertex Step 2 Finding two points to left of axis of symmetry Step 3 Reflecting two points to get points right of axis of symmetry Step 4 Plotting the Points (with table) Step 5 Graphing the Parabola In order to graph , we can follow the steps Step 1) Find the vertex (the vertex is the either the highest or lowest




Which Equation Matches The Following Parabola Y X Gauthmath




Find The Vertex Of The Parabola Y 2x2 10x 8 Brainly Com
Given the equation of a parabola in standard form ∙ xy = ax2 bx cx;Graph y=2x^212x10 y = −2x2 12x − 10 y = 2 x 2 12 x 10 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for − 2 x 2 12 x − 10 2 x 2 12 x 10 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find theThis video shows how to take the graph of y = x^2 and stretch it vertically by a factor of 2



Instructional Unit The Parabola Day 4 And 5



Answered Sketch The Parabola And Line On The Bartleby
Question Find the vertex of the parabola represented by the equation y=2x^224x100 Answer by Algebraic(50) (Show Source) You can put this solution on YOUR website!Every parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equationFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience parabolaequationcalculator y=2x^{2} en Related Symbolab blog posts My Notebook, the Symbolab way




Content Transformations Of The Parabola




4 Given Y2x2 4x4 See How To Solve It At Qanda
where (h,k) are the coordinates of the vertex and a is a multiplier to obtain this form use the method of completing the square ∙ the coefficient of the x2 term must be 1 ⇒ y = − 2(x2 − 6x 13 2) ∙ add/subtract (1 2 coefficient of the xterm)2 to x2 −6xCreate your account View this answer y = 2x25x−3 y = 2 x 2 5 x Actually, these parabolas won't "approach any axis asymptotically" A parabola's axis is the line that cuts the parabola into 2 equal halves (so each parabola cuts its axis once only, at the vertex) Probably the best you can do in terms of expressing these as one equation is to settle for 2 (zx)^2 = y^2 will give your 1st and 4th equations
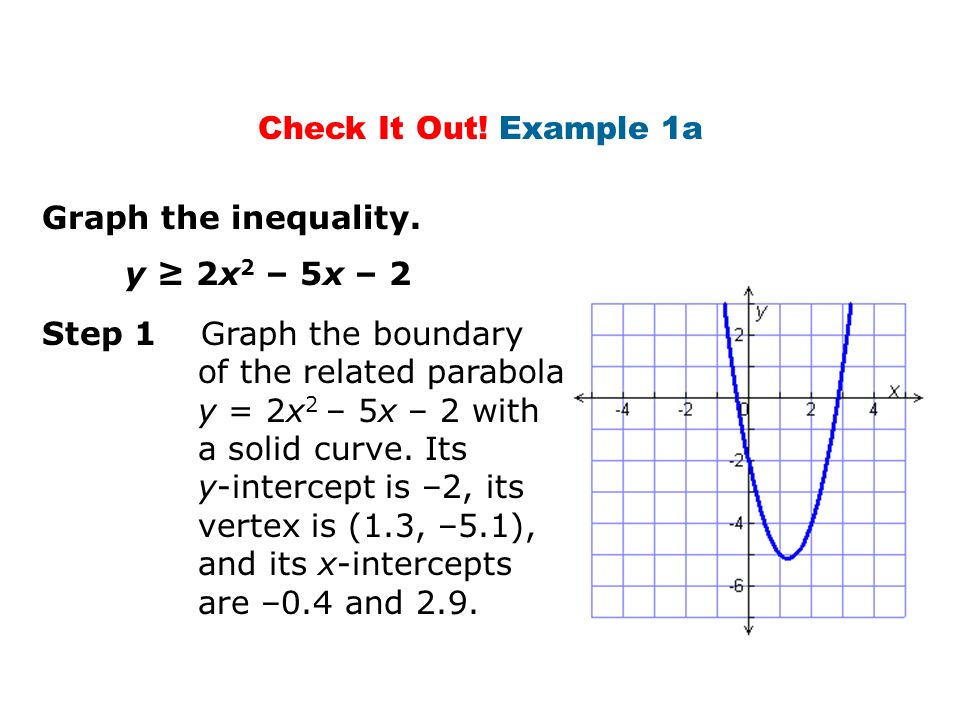



Warm Up 1 Graph The Inequality Y 2x 1 Solve Using Any Method 2 X 2 16x 63 X 2 8x 3 7 Ppt Download




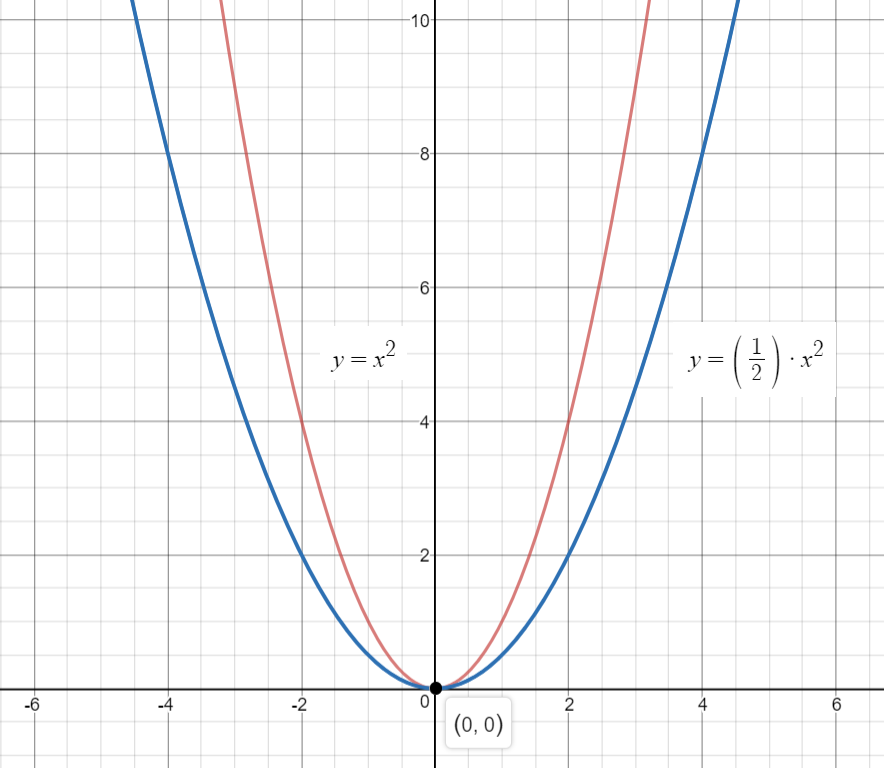
Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
EN parabolafunctionvertexcalculator menu Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Mean, Median & Mode Scientific Notation Arithmetics Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSee all questions in Vertical Shifts of Quadratic Functions



Draw The Graph Of Y 2x 2 1 And Heance The Graph Of F X Cos




What Is The Area Enclosed By The Parabola Y2 2x And The Line Y 2x Quora
Consider quadratic function whose parabola is described by \y = 2x^2 4x 6\ State whether this parabola's vertex is a maximum, or a minimum Find the coordinates of this parabola's vertexI have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I haveRemember that a quadratic equation can be derived from The equation you
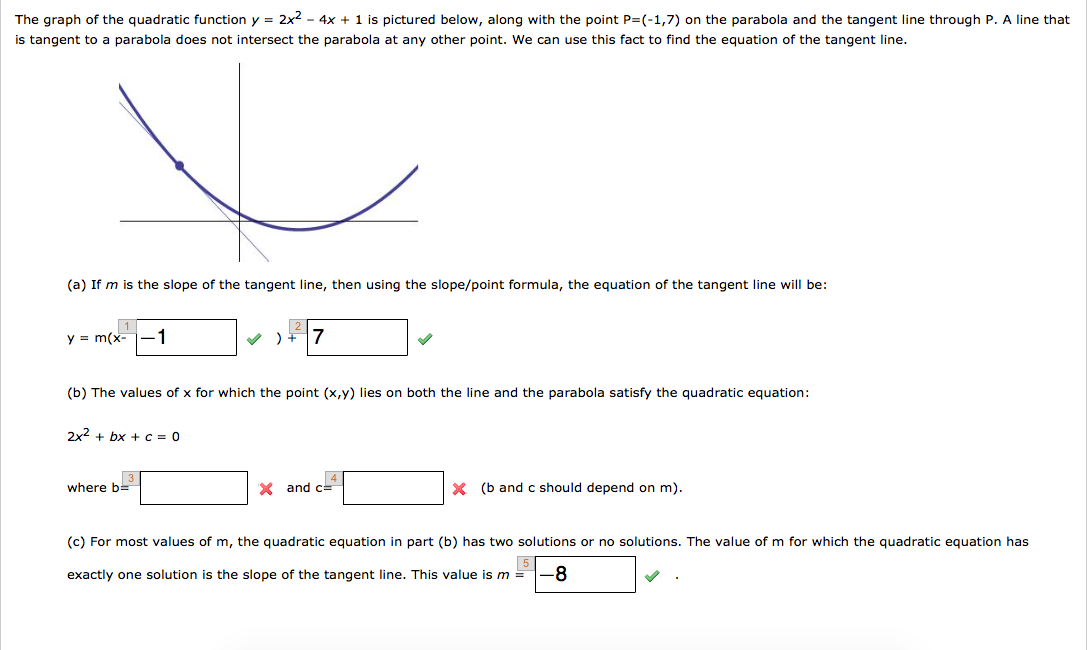



The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com



Graphing And Properties Of Parabolas Kuta Software
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW The focus of the parabola `y = 2x^2 x` isParabola, Finding the Vertex 41 Find the Vertex of y = 2x 2 3x5 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 2 , is positive (greater than zero)Precalculus Find the Vertex y=2x^2 y = 2x2 y = 2 x 2 Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 2 x 2 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 2, b = 0, c = 0 a = 2, b = 0, c = 0



Parabolas And Cubics



Find The Area Bounded By The Parabola Y 2 4x And The Line Y 2x 4 Sarthaks Econnect Largest Online Education Community
First we solve the 2 equations to find where the parabola and line intersect y^2= 2x=y On solving we get y=0,x=0 and y=1,x=1/2 The picture is like this The shaded region is now the required area So by using integral calculus of areas Integrate √ (2x) 2x putting limits 0 to 05To find the directrix of a parabola wohse equation is ##y=ax^2bxc## you can use this formula ##y= (1(b^24ac))/(4a)## So in case of this parbola ##y=2x^2##Graph y=2x^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or down




Mfg Graphing Parabolas




Graphing Parabolas
What is the vertex of the parabola represented by the equation, y=2x^ {2}24x100You can put this solution on YOUR website!The equation of the parabola #y=x^2# shifted 5 units to the right of equation, what is the new How do you sketch the graph of #y=3x^2# and describe the transformation?




Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Parabola Sketching Y 2x 2 4x 6 From The Parabola Translation Download Scientific Diagram
In mathematics, a parabola is a plane curve which is mirrorsymmetrical and is approximately UshapedIt fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves One description of a parabola involves a point (the focus) and a line (the directrix)The focus does not lie on the directrix The parabola is the locus of points inAlgebra Find the Vertex y=2x^28x2 y = 2x2 8x − 2 y = 2 x 2 8 x 2 Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 8 x − 2 2 x 2 8 x 2 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 2, b = 8, c = − 2 a = 2, b = 8, cY=2x^2 What is the vertex?



Exploration Of Parabolas




How To Graph A Parabola 13 Steps With Pictures Wikihow
We're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of a to determine how the graph changes



How Do You Graph Y 2x 2 4x 3 Mathskey Com



Organize The Information For Your Parabola Graph Your Parabola Y 2x 2 12x 19 Axis Of Symmetry Snapsolve




Area Enclosed By The Parabola Y 2 8x And The Line Y 2x Is A




Draw The Graph Of Y 2x 2 And Hence Solve 2x 2 X 6 0




How To Draw Y 2 X 2



Quadratic Graph Example Y Ax C Expii




Ex 8 2 7 Area Lying Between Y2 4x And Y 2x Is Ex 8 2




Content Transformations Of The Parabola



1




How To Graph A Parabola 13 Steps With Pictures Wikihow



Exploration Of Parabolas



Www D105 Net Cms Lib Il Centricity Domain 610 Vertex practice worksheet answers Pdf



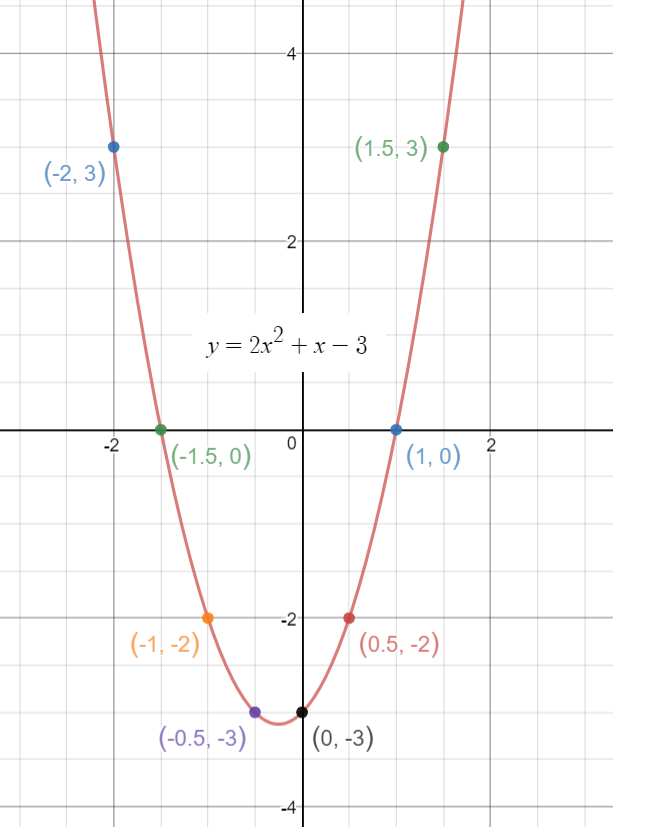
Draw The Graph Of Y 2x 2 3x 5 And Hence Solve 2x 2 4x 6 0 Y 2x 2 3x 5 Sarthaks Econnect Largest Online Education Community




Find The Area Of The Region Enclosed By Chegg Com




Solution Find The Equation Of The Axis Of Symmetry Of The Function Y 2x 2




4 Given Y2x2 4x4 See How To Solve It At Qanda




Graph The Parabola Y 2x 2 4x 1 Youtube



Untitled Document



Graphing Quadratic Functions



1



Parabola Investigation In This Task We Will Investigate The Patterns In The Intersections Of Parabola And The Lines Y X And Y 2x International Baccalaureate Maths Marked By Teachers Com



How Do You Sketch The Graph Of Y 1 2x 2 And Describe The Transformation Socratic



Solution I Have To Find The Vertex Axis Of Symmetry Minimum Or Maximum Value And Range Of The Parabola The Formula Is Y Ax 2 Bx C Question Y 2x 2 6x 3 What I Have So Far Y 2x 2 6x




Sketch The Parabola Math Y 2x 2 6x 4 Math By Using Its Intercepts Homework Help And Answers Slader



For What Values Of B Will The Straight Line Y 2x B Not Intersect The Parabola Y X 2 3x 5 Math Homework Answers



1




Find The Points On The Parabola Y 2x 2 6x 4 At Which The Tangent Is Parallel To The X Axis



How To Do You Graph Y 2x 2 X 3 By Plotting Points Socratic
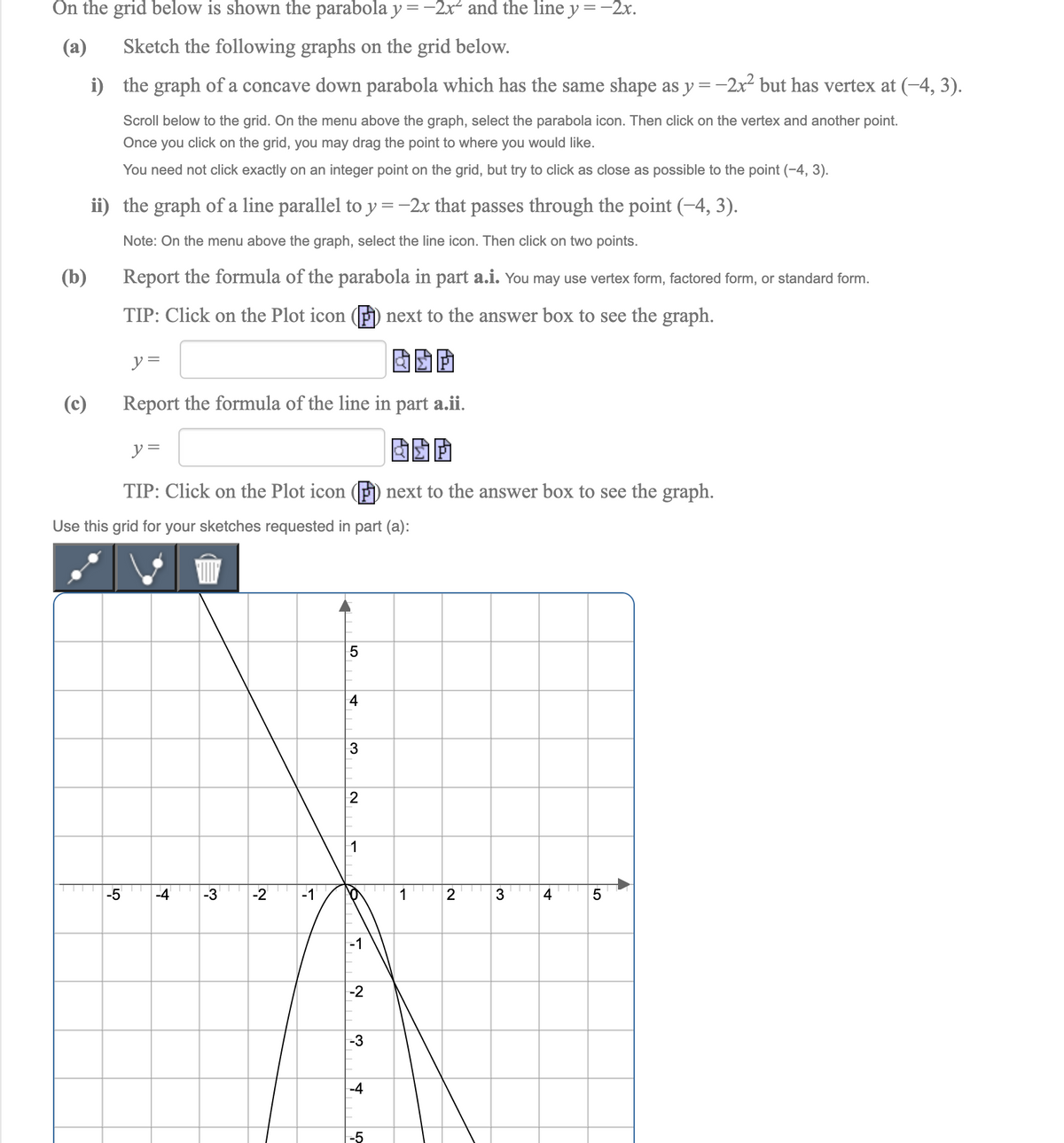



Answered On The Grid Below Is Shown The Parabola Bartleby
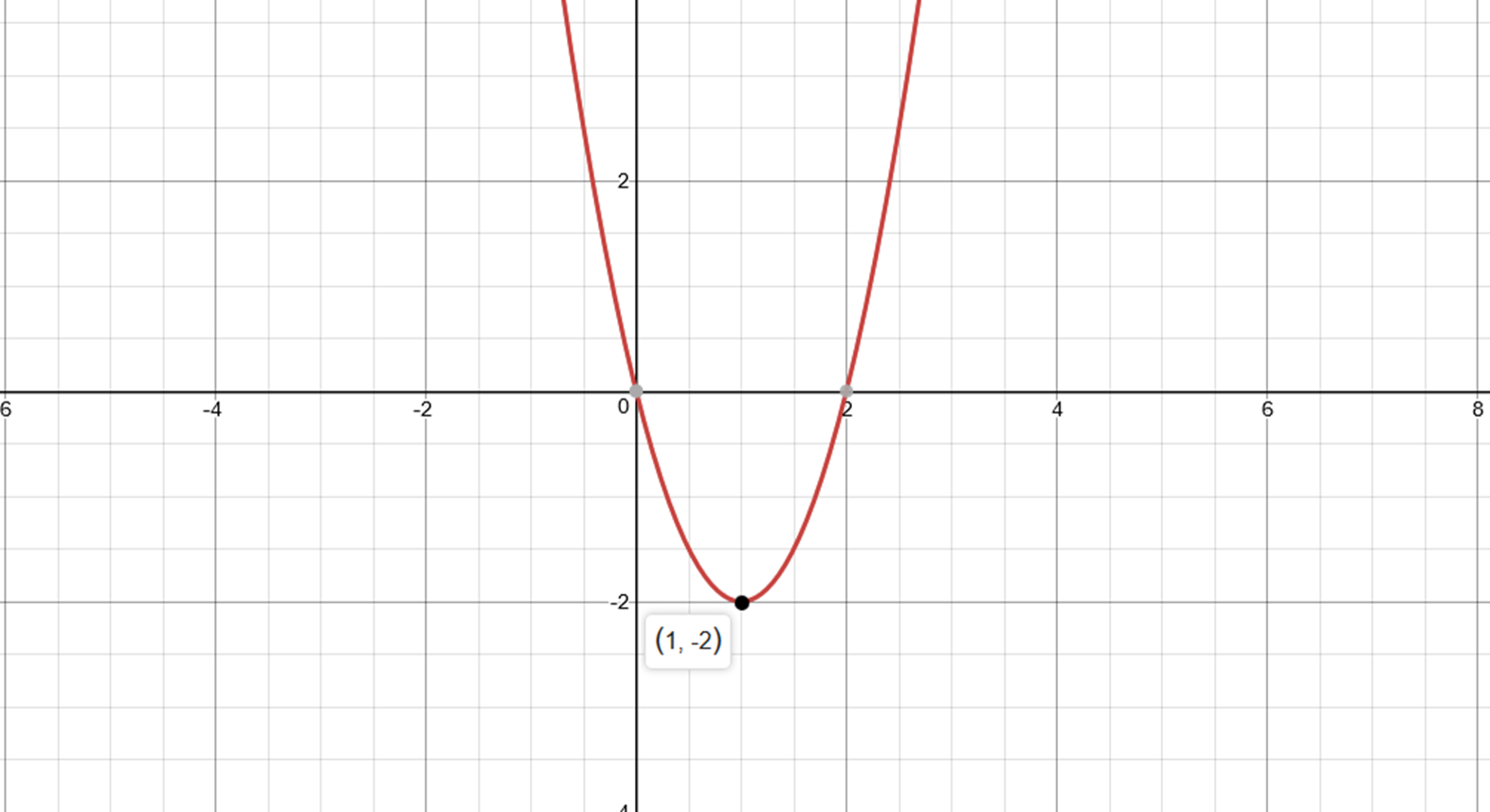



How Do You Find The Vertex Of Y 2x 2 4x Socratic




The Aim Of This Powerpoint Is To Enable You To Quickly And Easily Draw The Graphs Of Parabolas When Given Their Equations It Will Show You How To Determine Ppt Download



Untitled Document
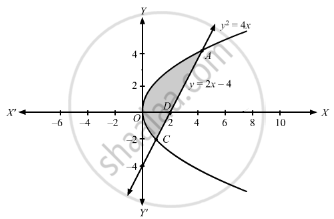



Find The Area Bounded By The Parabola Y2 4x And The Line Y 2x 4 I By Using Horizontal Strips Ii By Using Vertical Strips Mathematics Shaalaa Com
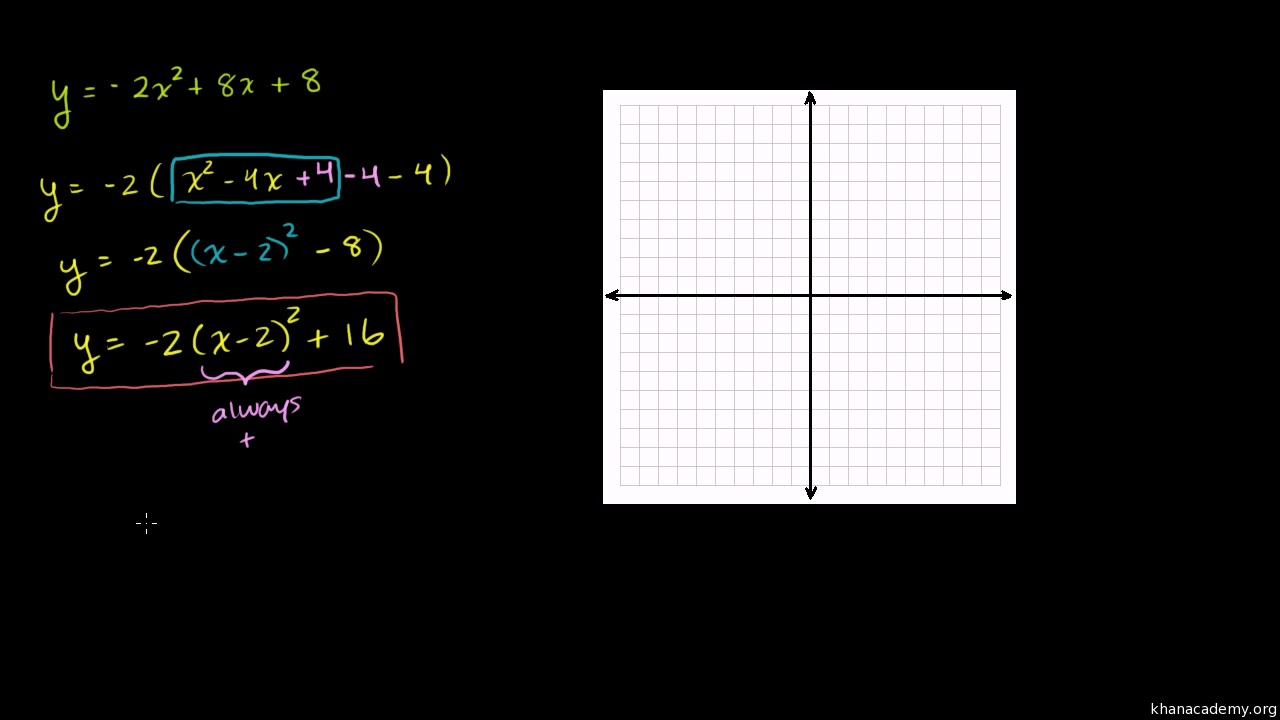



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy




Please Help Asap Correct Answer Only Please The Graph Of The Function Y X2 Is Shown How Brainly Com
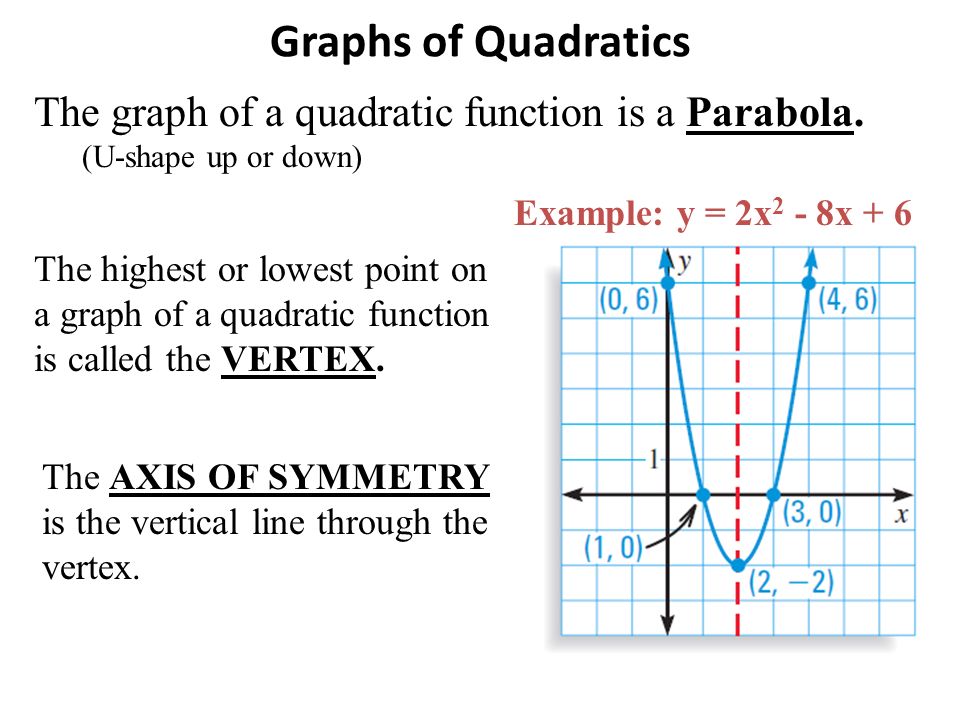



Warm Up Graphing Using A Table X Y 3x 2 Y 2 Y 3 2 2 8 Y 3 1 Y 3 0 Y 3 1 Y 3 2 2 4 Graph Y 3x Ppt Download




Quadratic Function



Ny Schoolwires Net Cms Lib Ny Centricity Domain 196 Algebra i Regents review Jmap worksheets A G 5 Stretchingquadraticfunctions Pdf
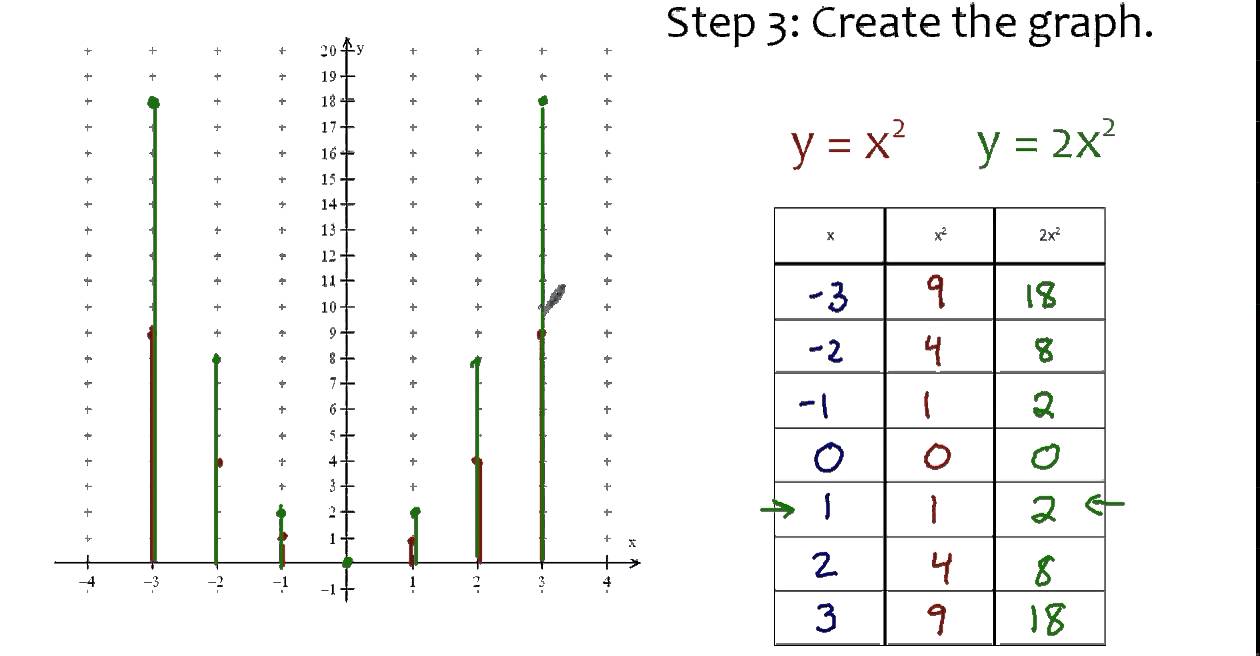



Y 2x 2 Youtube




Y X 2
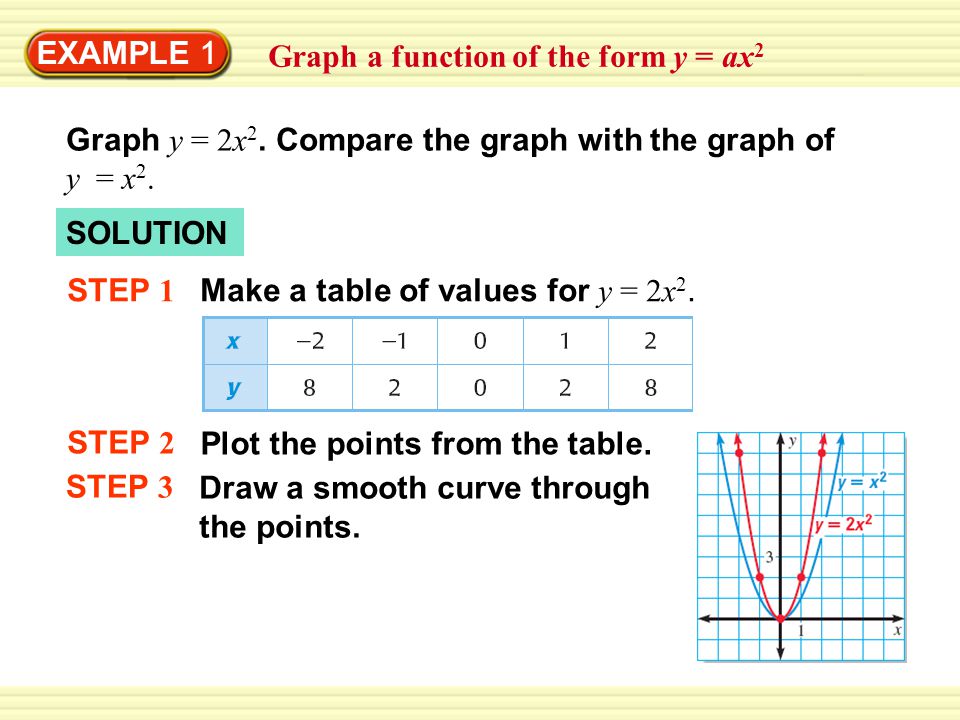



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download
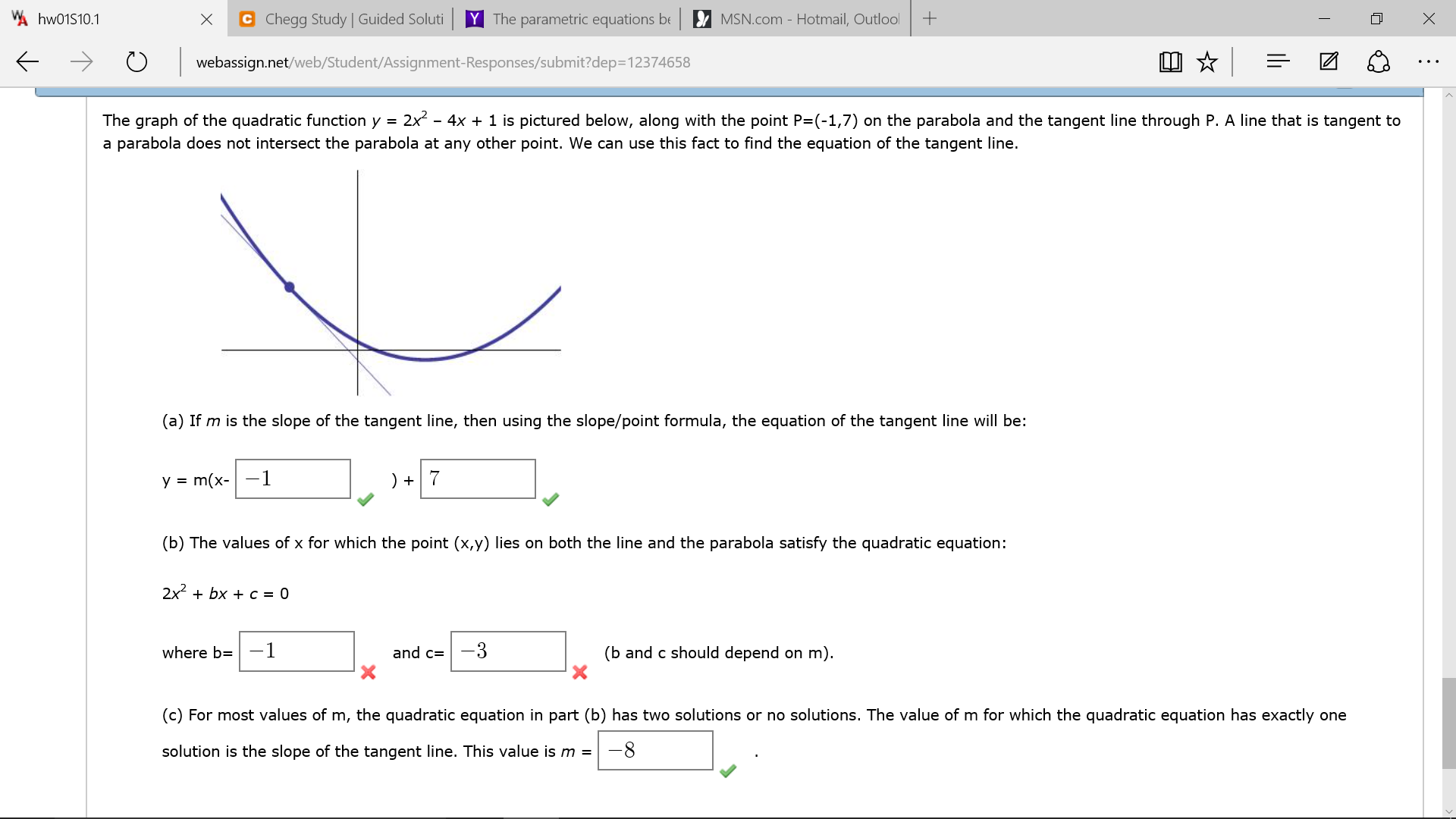



The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com



What Is The Nature Of The Graph Y2x2 A Parabola Passing Class 11 Maths Cbse




6 The Graph Of The Parabola Given By The Function Y 2x2 2x 1 Opens Up Or Down Incorrect Your Answer Down Correct Answer Down Explanation The 2 In Y 2x2 2x 1




Graphing Parabolas




Y 2x 3 Y 3x 2 Graph Novocom Top



Solution Graph Y 2x 2 4x



1




Sketch The Region Enclosed By The Curves Y 2x 2 And Y 4 X 2 Draw A Typical Approximating Rectangle And Label Its Height And Width Setup But Do Not Evaluate



Parabolas And Cubics




Y 2x 2 Parabola Novocom Top



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively
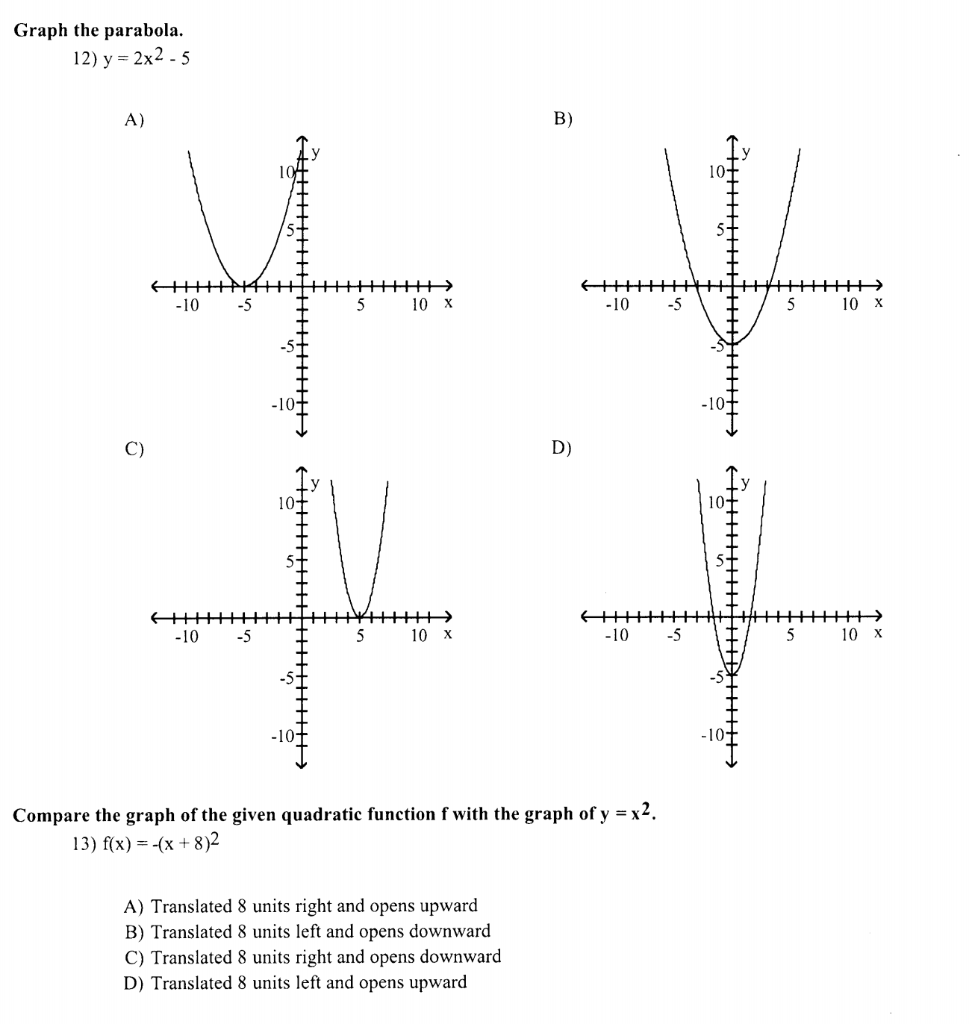



Solved Graph The Parabola 12 Y 2x2 5 A B 10h 10 4 Chegg Com
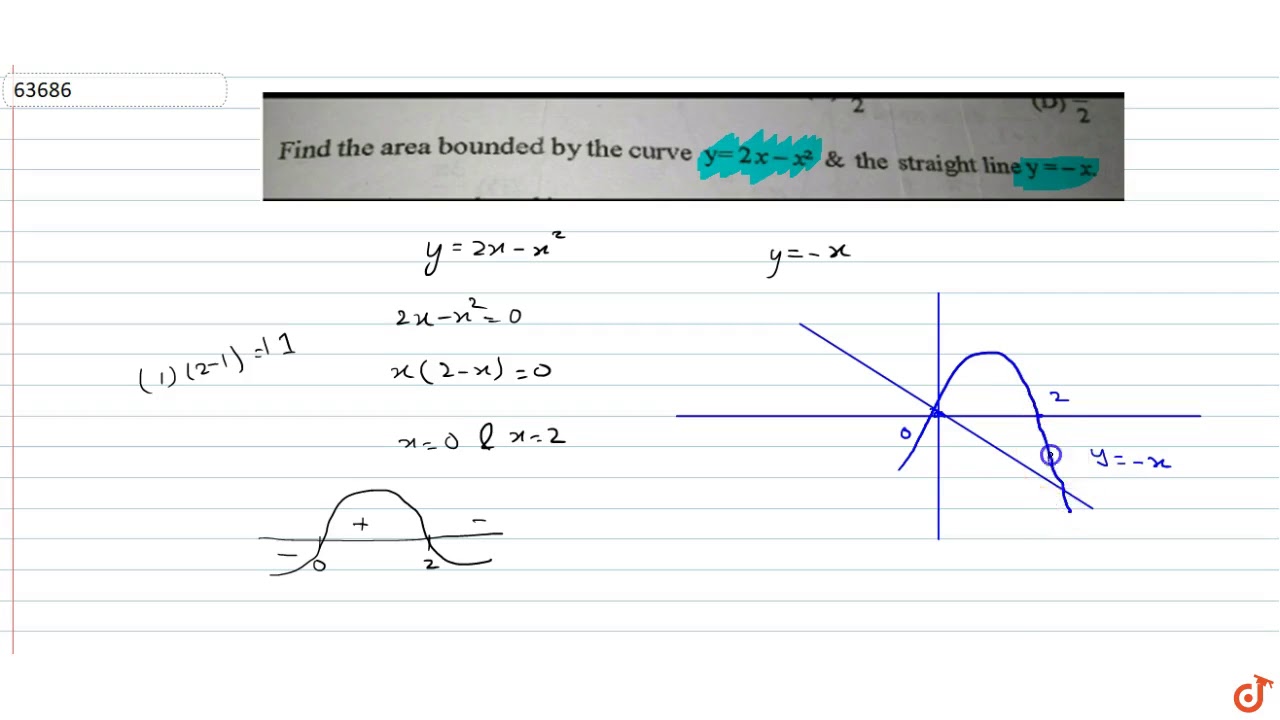



Find The Area Bounded By The Curve Y 2x X 2 And The Straight Line Y X Youtube




What Is The Maxima And Minima Global And Local Of The Function Y 2x X 2 Explain It With The Help Of A Graph Quora




Graph The Quadratic Functions Y 2x 2 And Y 2x 2 4 On A Separate Piece Of Paper Using Those Graphs Compare And Contrast The Shape And Position Of The Graphs Study Com



Mathscene Functions 1 Lesson 3
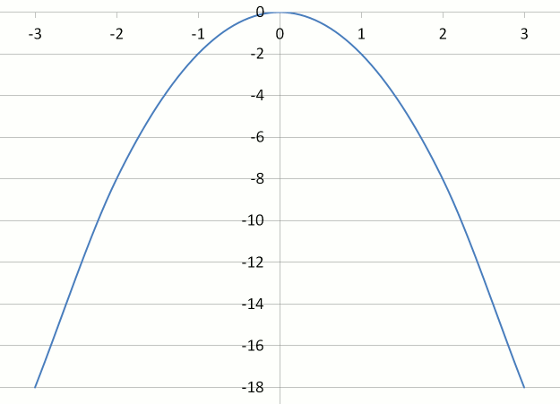



Parabolas Xcelerate Math



Solution Find The Vertex Of The Parabola Y 2x2 12x 13




Graph The Parabola And Give Its Vertex Axis X Intercepts And Y Intercept Y 2x 2 8x 16 Study Com



Quadratics Graphing Parabolas Sparknotes



Solution Y 1 2x 2 Graph The Parabola Plot The Vertex And Four Additional Points Two On Each Side Of The Vertex



Draw The Graph Of Y 2x 2 X 6 Mathskey Com




Solution Find The Equation Of The Axis Of Symmetry Of The Function Y 2x 2 7x 5



What Is The Vertex Of Y 2x 2 4x 12 Socratic




Parabel Y 2x 2 Novocom Top
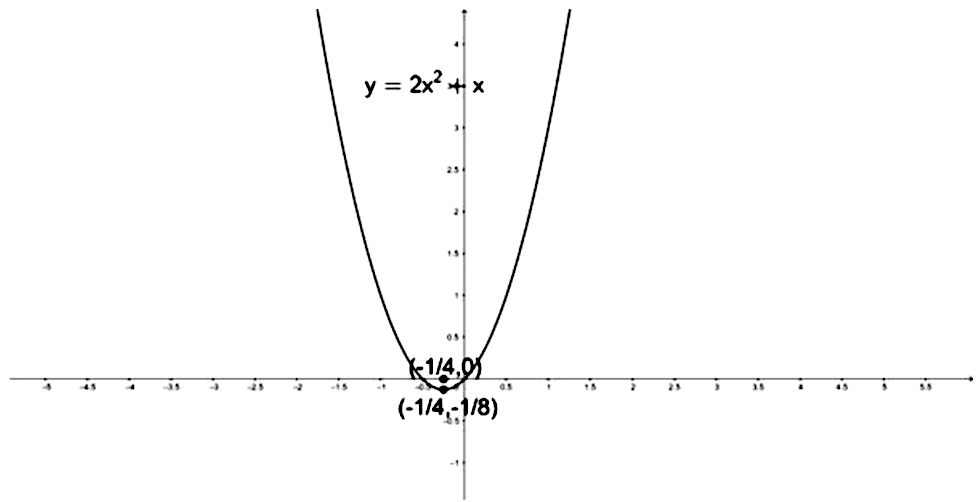



The Focus Of The Parabola Y 2x 2 X Is A 0 0 B 1 2 1 4 C 1 4 0 D 1 4 1 8 Snapsolve



Quadratics Graphing Parabolas Sparknotes
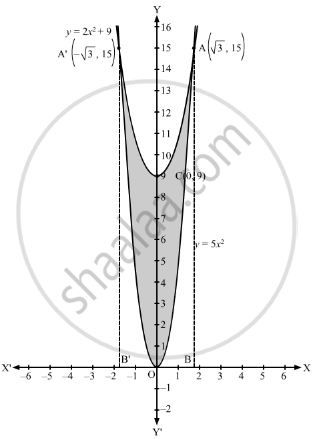



Find The Area Enclosed By The Parabolas Y 5x2 And Y 2x2 9 Mathematics Shaalaa Com




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
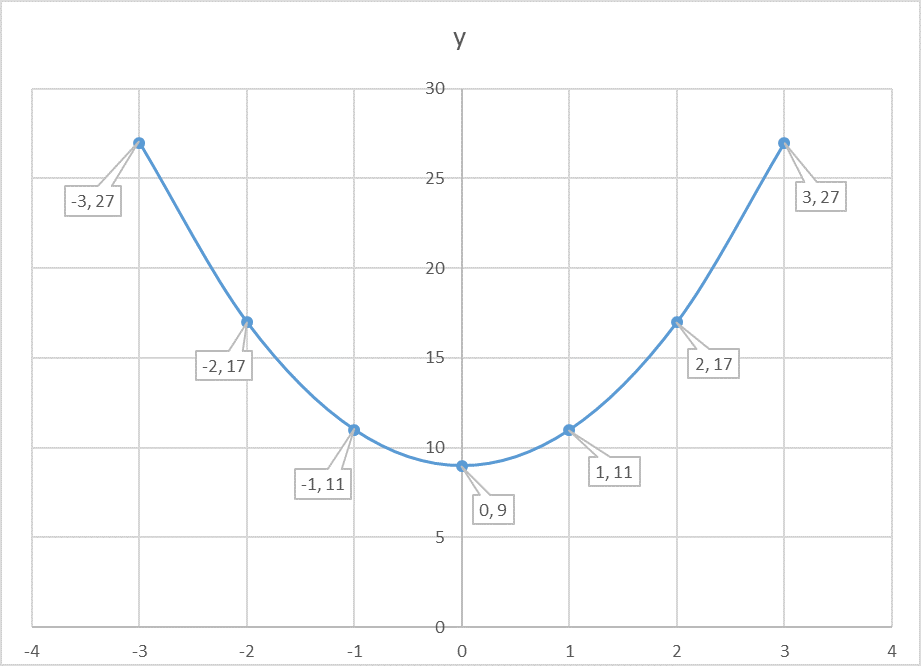



How Do You Graph The Parabola Y 2x 2 9 Socratic
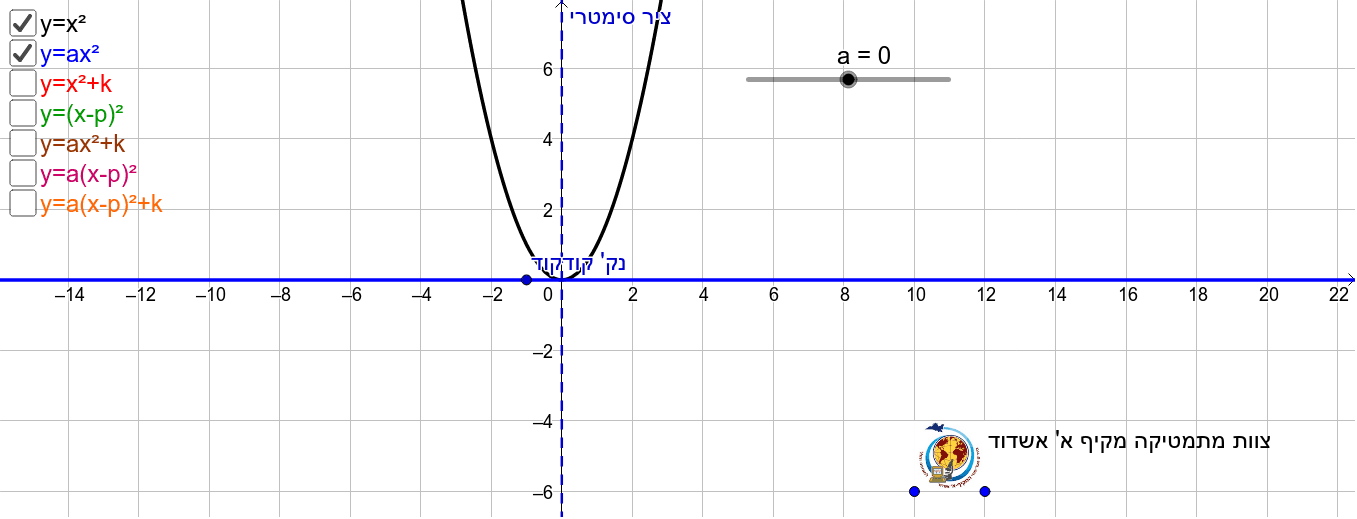



Parabola Y X 2 Geogebra



Solution Graph The Quadratic Equation Y 2x 2 What Is The Vertex Also Graph The Parabola If You Can Please Include The Points That I Have To Graph Plot That Would Be G




Q15 The Area Common To The Parabola Y 2x2 And Y X2 4 Is




Focus Of Parabola Y 2x 2 X
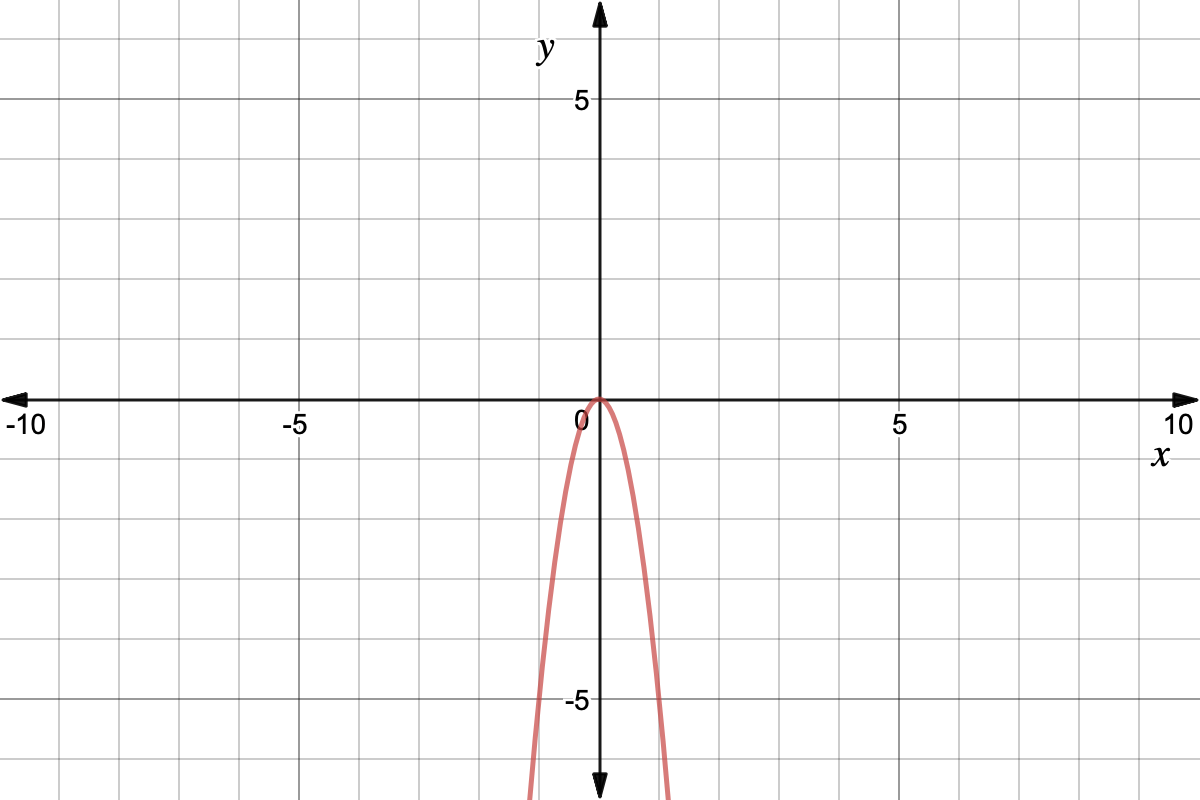



Quadratic Graph Example Y Ax Expii


